How to Solve Ratios: Problems, Questions and Examples
All products and services featured are independently selected by WikiJob. When you register or purchase through links on this page, we may earn a commission.
Ratio Meaning
A ratio is a mathematical term that is used to compare the size of one number to the size of another number. It is commonly used in both mathematics and in professional environments.
Here are some everyday examples of times when you could use ratios:
- When you convert your Pounds to Dollars or Euros when you go on holiday
- When you calculate your winnings on a bet
- When you work out how many bottles of beer you need for a party
- When you share a packet of sweets fairly among your friends
- When you calculate how much tax you must pay on your income
Ratios are usually used to compare two numbers, though they can also be used to compare multiple quantities.
Ratios are often included in numerical reasoning tests, where they can be presented in a number of different ways. It is therefore important that you are able to recognize and manipulate ratios however they are presented.
Variable Ratio Example
Ratios are usually shown as two or more numbers separated with a colon, for example, 8:5 or 1:4 or 3:2:1.
However, they can also be shown in a number of other ways; the three examples below are all different expressions of the same ratio.

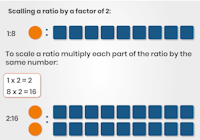
Scaling a Ratio
One of the reasons that ratios are useful is that they enable us to scale amounts. This means increasing or decreasing the amount of something. This is particularly handy for things like scale models or maps, where really big numbers can be converted to much smaller representations that are still accurate.
Scaling is also helpful for increasing or decreasing the amount of ingredients in a recipe or chemical reaction. Ratios can be scaled up or down by multiplying both parts of the ratio by the same number.
For example:
There are six practice questions below. Should you need further practice afterwards, we recommend the numerical reasoning packages available from JobTestPrep. These tests include ratio questions, with full explanations for all answers.
Prepare for Any Job Assessment Test with JobTestPrep
Olivia wants to make pancakes for nine friends, but her recipe only makes enough pancakes for three friends (the recipe is shown below).
What quantity of the ingredients will she need to use?
Pancake recipe (serves 3)
- 100g flour
- 300ml milk
- 2 large eggs
Prepare for Any Job Assessment Test with JobTestPrep
Reducing a Ratio
Sometimes ratios are not presented in their simplest form, which makes them harder to manipulate.
For example, if a farmer has seven chickens and together they lay 56 eggs every day, this would be represented by the ratio 7:56 (or presented as a fraction this would be shown as 7/56).
Reducing a ratio means converting the ratio to its simplest form, and this makes it easier to use. This is done by dividing both numbers in of the ratio by the largest number that they can both be divided by (this is just the same as reducing a fraction to its simplest form).
So, for example:

Therefore, the reduced ratio is 1:8, which tells us that each chicken lays eight eggs. This is far easier to use. For example, if the farmer needed 96 eggs per day, he could use the ratio to work out how many chickens he would need for this to be possible.
We know from the ratio that each chicken lays 8 eggs, therefore, if the farmer wants 96 eggs he must divide 96 by 8 to calculate the number of chickens required:
96/8 = 12 chickens
Similarly, if one of the farmer’s chickens stopped laying eggs, he could use the ratio to work out how much that would reduce his total number of eggs to; for example, 56 – 8 = 48.
Prepare for Any Job Assessment Test with JobTestPrep
Ella has 18 pigeons and they eat 54kg of grain per week. Jayden has 22 pigeons and they eat 88kg or grain per week. Who has the greediest pigeons?
If you need to prepare for a number of different employment tests and want to outsmart the competition, choose a Premium Membership from JobTestPrep.
You will get access to three PrepPacks of your choice, from a database that covers all the major test providers and employers and tailored profession packs.
Prepare for Any Job Assessment Test with JobTestPrep
Finding Unknown Quantities From Existing Equivalent Ratios
One of the ways that ratios are particularly useful is that they enable us to work out new and unknown quantities based on an existing (known) ratio. There are a couple of ways of solving this type of problem. The first is to use cross-multiplication.
For example, there are four rings and seven bracelets in the jewellery box. If this ratio were maintained, how many necklaces would there be if there were 28 bracelets?

Another method is to calculate the factor (size) of the increase in number of bracelets (28/7 = 4) and to then multiply the number of rings by that same number (4 x 4 = 16).
Question 3: Finding Unknown Quantities From Existing Equivalent Ratios
Gabriel and Mandeep are getting married. They have calculated that they will need 35 bottles of wine for their 70 guests. Suddenly they find out that another 20 guests are planning to attend.
How much wine do they need in total?
Common Mistakes and Things to Look Out For When Solving Ratio Problems
-
Make sure you are reading the ratio the right way. For example, a ratio of 2 pink to 6 red should be expressed 2:6 not 6:2. The first item in the sentence comes first.
-
Be careful with reading the wording. For example, people often make mistakes with questions such as “Bob has eight pigs and four cows. Calculate the ratio of pigs to animals.” It can be tempting to say the ratio is 8:4, but that would be incorrect because the question asks for the ratio of pigs to animals. Therefore you need to calculate the total number of animals (8 + 4 = 12), so the correct ratio is, therefore, 8:12 (or 2:3).
-
Don’t be put off by units or decimals. The principles remain the same whether they apply to whole numbers, fractions, £ or m2, but do ensure you note the units in your calculations, and where possible convert them to the same units. For example, if you have a ratio of 500g to 0.75kg, then convert both sides to either grams or kilos.
Prepare for Any Job Assessment Test with JobTestPrep
Otto knows that his car requires 27.5 litres of fuel to drive 110 miles. He wants to drive from London to Edinburgh, a distance of 405 miles.
How much fuel will he need?
Hugo and Claudia share 600 g chocolate using the ratio 4:2.
How much chocolate does Claudia get?
Caleb wants to paint his house. He checks the instructions on the paint tin and finds that one tin of paint will cover 5m2. The total wall area Caleb needs to paint is 40m2. How many tins of paint will he need to buy?
If you would like to practise more ratio-based questions, WikiJob has a psychometric tests app, available in both iTunes and Google Play. All tests include a timer and worked solutions at the end. Give it a try!
Additional Example Questions
What is the ratio of 2 to 4?
What is the ratio of 2 and 3?
What is a 2 to 1 ratio example?
How do you find the ratio of 1/2 to 2/5?
To easily solve a ratio question first add all the parts of a ratio together to find the total number.
For example, if you have to split 20 sweets into a ratio of 3:1, you add the ratio figures up to find the total.
In this case, that’s 3 + 1 = 4.
The second step is to divide the number of sweets you are working with by the total you found. So 20 sweets divided by 4 equals 5.
That 5 is then used in the third and final step to create the answer.
The first number in the ratio is 3 so you multiply the 5 by 3. This gives 15. The second number in the ratio is 1 so you multiply the 5 by 1 to get 5. That gives you a final ratio of 15:5 or 20 sweets split into a pile of 15 and a pile of 5.
A common mistake people make in ratio questions is getting the numbers the wrong way around. For example, when talking about there being 5 weekdays to 2 weekend days, you would express that as 5:2. The first item being mentioned comes first in the ratio, regardless of which number is bigger.
Another common mistake in ratio questions is misreading the information, so always take care to read thoroughly before rushing to answer.
A third common mistake in ratio questions is being thrown off by units or decimals. The principles of ratios remain the same regardless – but do convert km to meters, for example, so that you’re working in the same size unit for both sides of the ratio.
There are a few different types of ratio questions you can get. The first thing you want to do is to assess which type of question it is – for example, it could be a scaling question, a reduction of ratios or finding an unknown quantity from an existing ratio.
Once you work out which type of question it is you can get an answer in minutes.
A scaling question almost always just involves multiplying or dividing the original ratio numbers. Reducing a ratio requires working in fractions and might just require dividing the original ratio by half or another number. The last type of ratio question, which requires finding an unknown quantity, can require cross-multiplication or simple algebra.
The best way to prepare for ratio questions for bank or other competitive exams is to practice them and to refresh all your basic mathematical principles. This will build your confidence and speed.
In terms of tricks, it helps to remember that the main property of ratios is that they need to exist between like quantities (for example, the same units and type, so that you’re comparing kg to kg or lbs to lbs).
The other main property of ratios to remember is that all parts of it must be multiplied or divided by the same quantity. So if you are doubling a recipe, for example, all parts of it must be increased by a factor of two.
A simple ratio question might be working out the ratio of boys and girls in a class. If there are 10 boys and 12 girls you could divide each number by a common denominator (in this case 2). So you get the answer that there's a 5:6 ratio of boys to girls.
This is an example of a ratio reduction. An example of a scaling question could be: “If 10 liters of fuel are needed to drive 50 miles, how much is needed to drive 200 miles?” In this case, you can see that the mileage has increased 4 times, therefore the fuel amount also needs to be multiplied by 4, – giving an answer of 40 liters.
In terms of definitions, a ratio is an ordered pair of numbers, such as a and b, often written a:b. So to answer the question of whether ratios perform a proportion, you could say that they do show the proportions of a versus b.
For example, if we are talking about how many smokers there are in an office you could say that the ratio is 1:10. That would mean there is one smoker to every 10 non-smokers – and this ratio is the most simplified way to look at the numbers.
As a proportion, that same concept would be expressed as 1/10. If the office was bigger, you might say that the proportion is 10/100. Each of these two fractions (1/10 and 10/100) is equivalent to the same proportion.
Ratios are used in everyday life in various ways. For example, you might be on a diet 6 days a week and have 1 cheat day. That would be expressed as a 6:1 ratio.
Ratios are also used when traveling. For example, if you needed to convert British Sterling from US Dollars it might help you to know that the ratio is 1:1.4 when shopping. That way you can work out what you’re spending in your home currency versus just the travel currency.
Another everyday use of ratios can happen if you are planning a party and you predict most people will drink 3 beverages. You could then use ratios to work out how much to buy. If 15 people are coming, for example, you would then use ratios and multiply by 3 to buy 45 beverages.
Ratios are typically presented with colons. They can also be seen in using fractions or the word ‘to’.
For example, a 1:2 ratio could be expressed as 1/2 or with the words '1 to 2'.
In terms of basic rules, you need to treat each side of the ratio the same way. For example, if you’re tripling one side of a ratio, you would do the same to the other side.
Another rule is that ratios should exist between quantities of the same kind, such as mm to mm or kg to kg. You can always adjust the units to match – for example, if you were given two items, one in grams and one in kg you can multiply the latter by 1,000 to turn both items into gram measurements.
If you are studying mathematics, any related scientific disciplines or even a subject like Geography then having a grasp of ratios and proportions will be helpful.
For example, you might be asked to work out the ratio of white sand beaches to black sand beaches in the world, so being able to manipulate data in these simple ways is a useful skill to have.
Also, when it comes to applying for jobs or internships as a student, you will need to prepare for assessment tests. These often include numerical reasoning tests, where ratios and proportions can be presented in several different ways.
As a student, it is therefore important that you can recognize and work with data to make the best of the next steps in your career.
Not much prior knowledge is needed to solve ratios, but it helps if you are comfortable with numbers and basic mathematical concepts.
If you have previously studied fractions or algebra then the concept of ratios is easier to grasp. Even basic human constructs such as sharing food fairly between people can be helpful to give ratios a context that is relatable.
For example, the knowledge of how to share a box of chocolates between five people can be useful to understand ratios. If there are 30 chocolates in the box you can describe the distribution of them in a ratio of 6:1 – so 6 chocolates are given per person.
It helps to make the examples easy to grasp when teaching students ratios. For example, you can talk about a family that has one cat and two dogs. The ratio of cats to dogs is therefore 1:2.
Giving as many examples as possible from real life will make it more straightforward to teach a student about ratios. Simple examples will make it easier for them to understand ratios and you can also relate ratios to the concept of fairness – as students often care a lot about this.
For example, you could say that in the school next door the teacher-to-student ratio is 1:10. You could compare this to the school you are in and ask them whether it’s fair that the ratio is different in one learning environment versus another.
When scaling up a recipe while cooking you might use ratios. For example, a common shortbread recipe uses flour, sugar and butter in a 4:2:1 ratio of cups.
If you wanted to make double the amount of shortbread you were originally making, you would then use 8 cups of flour, 4 cups of sugar and 2 cups of butter.
Therefore just doubling the initial measurements is a way of using ratios.
Using ratios this way removes the need to remember exact weights or measurements, which is helpful when you don’t have a scale to hand.
Learning commonly-used ratios like the amount of flour to liquid when making bread or fritters, can result in more powerful and intuitive cooking skills than slavishly following a recipe each time would.






