How to Calculate Percentages and Solve Percentage Questions (2025 Guide)
All products and services featured are independently selected by WikiJob. When you register or purchase through links on this page, we may earn a commission.
- What Is a Percentage?
- Types of Percentage Problems
- Is It Important to Learn About Percentages?
empty
empty
empty
- Converting Decimals and Fractions to Percentage Values
- How to Work Out the Percentage of a Known Value
empty
- Calculating What Percentage One Number is of Another Number
empty
- How to Work Out a Percentage Increase
empty
- How to Work out a Percentage Decrease or Discount
- Working Backwards From a Percentage
empty
- Common Mistakes and Things to Look out For When Solving Percentage Questions
What Is a Percentage?
A percentage is a way of calculating how much there is of something in relation to the whole.
Percentages are used very widely in both mathematics and everyday situations, and they are really useful for understanding relative amounts and making them meaningful.
Types of Percentage Problems
Here are some common ways that percentages are used in day-to-day life:
- Calculating how well a student has performed on a test
- Working out how much VAT you need to pay on a purchase
- Calculating how much to leave as a tip in a restaurant
Is It Important to Learn About Percentages?
Yes, learning about percentages is important as it is a fundamental concept in mathematics and everyday life.
Percentages are used in a wide range of contexts, including business, finance, statistics, science and everyday calculations.
Here are a few more reasons why understanding percentages is important:
- Real-world applications
- Data interpretation
- Problem solving
- Comparisons and ratios:
- Business and finance
- Communication and interpretation
- Personal finances
Percentages are usually represented by the % symbol, and there are a few basic rules you need to understand to be able to manipulate percentages:
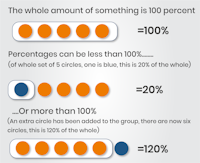
Percentages are widely used in numerical reasoning tests, so it is important that you are able to understand and interpret them effectively.
Prepare for Any Job Assessment Test with JobTestPrep
How to Add Percentages
If you are adding consecutive percentages, unfortunately it is not as simple as adding them together and then applying that number to the problem.
If you need to find the total of £200 + 10% + 15%, the initial thought might be to calculate £200 + 25%.
Instead, you need to calculate them separately and in order.
First, add 100 to each percentage and then convert it to make a decimal larger than 1:
10% becomes 110% which is converted to 1.10
15% becomes 115% which is converted to 1.15
The original value is then multiplied by these numbers.
To ensure that the number is manipulated correctly, the multiplication needs to be completed in the order that it is presented in the question:
200 x 1.10 = 220 – This is the first step: £200 + 10%
220 X 1.15 = 253 – This is the second step: (£200 + 10%) + 15%
Therefore, the answer to £200 + 10% + 15% is 253.
How to Multiply Percentages
To multiply percentages, you can convert them into decimals, multiply the decimals, convert back into a percentage.
For example, if you are asked to multiply 15% and 40% together, the calculation would look like:
15% = 0.15
40% = 0.40
0.15 x 0.40 = 0.06
0.06 x 100 = 6%
If you prefer to work in fractions, the calculation can also be done that way.
For example, if you need to multiply 10% by 30%, you would convert them into fractions out of 100 then simplify:
10% = 10/100 = 1/10
30% = 30/100 = 3/10
Then multiply each fraction together. There is already a common denominator:
1/10 x 3/10 = 3/100
Then convert the fraction back into a percentage:
3/100 = 3%
How to Subtract Percentages
To subtract one percentage from another, just ignore the percentage signs and treat them like whole numbers.
For example, to subtract 20% from 50%, perform the sum 50 – 20 to get 30. The answer is 30%.
If you are subtracting a percentage from a whole number, you first need to convert it to a decimal.
If you are asked to subtract 25% from 45 (for example, when calculating a discount), then you need to start by converting 25% to a decimal, which is 0.25.
To calculate the amount that should be subtracted, multiply the original number by the decimal:
45 x 0.25 = 11.25
Then subtract this amount from the base figure:
45 – 11.25 = 33.75
You can also take the decimal you converted the percentage into, subtract it from 1, then multiply the original number by it:
25% = 0.25
1 – 0.25 = 0.75
0.75 x 45 = 33.75
Converting Decimals and Fractions to Percentage Values
When taking a numerical reasoning test, you may be required to move fluidly between questions using percentages, fractions and decimals. It is very straightforward to convert numbers between these different representations, and these are key techniques to learn.
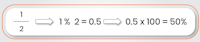
To translate fractions into percentages, you should divide the bottom number in the fraction by the top number.
This will give a decimal figure. Then multiply that decimal figure by 100, to create the percentage.
Here’s an example:
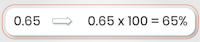
To translate decimals into percentages is even easier. Simply multiply the decimal figure by 100 to calculate the percentage:
Finally, to convert percentages into decimals is also very straightforward. You need to divide the percentage by 100 to calculate the decimal:

Prepare for Any Job Assessment Test with JobTestPrep
How to Work Out the Percentage of a Known Value
This is a particularly useful technique, as it allows you to work out how much of a whole value a particular percentage would be. This is the formula you would need to use:

This is something that people use all the time. For example, if you went out for dinner, spent £56 and wanted to leave a 10% tip, this is how you would work it out:
(£56/100) x 10 = £5.60
There are ten practice questions below. Should you need further practice afterwards, we recommend the practice packages available from JobTestPrep. These tests include percentages questions, with full explanations for all answers.
Question 1: Calculating the Percentage of a Known Value
Calculating the percentage of a known value is quite straightforward. In a numerical reasoning test, these questions tend to require you to identify/manipulate the relevant information in order to use the formula.
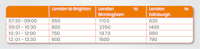
Graphs or tables will often be used to present the information, such as the one below.
Table 1: Passenger Numbers Using Rail Services at Different Times of Day
If you need to prepare for a number of different employment tests and want to outsmart the competition, choose a Premium Membership from JobTestPrep.
You will get access to three PrepPacks of your choice, from a database that covers all the major test providers and employers and tailored profession packs.
Prepare for Any Job Assessment Test with JobTestPrep
What percentage of passengers travelling between London and Brighton travelled before 12:01?
What percentage of the total passengers travelled from London to Edinburgh?
What percentage of passengers travelling between 10:31 and 12:00 were going to Birmingham?
Calculating What Percentage One Number is of Another Number
This allows you to work out what percentage of the total a particular value contributes. It is easiest to explain how to do this with an example.

Imagine you have 3 green apples (this is value A) and 5 red apples (this is value B). Together there are 8 apples, which is 100% of the apples you have.
What percentage of the apples are green?
In class 11b there are 12 girls and 18 boys. What percentage of the class are girls?
How to Work Out a Percentage Increase
Percentage increases are useful for understanding, for example, what an energy price hike means for you in financial terms, or to understand what a percentage rise in inflation equates to.
The formula you need to use to calculate this is:

So, if a family originally paid £1,000 per year for their energy, and their bill was increasing by £200, this is a 20% increase. The formula to calculate this is: (£200/£1,000) x 100 = 20%
Using percentages like this is also useful for comparing changes to different numbers, where it can be difficult to see at a glance what the impact has been.
Question 3: Percentage Increases
Car Insurance Costs

By what percentage did Tom’s car insurance increase between 2014 and 2016?
Whose car insurance increased by the greatest percentage between 2015 and 2016?
What is the lowest percentage increase in insurance incurred by any of the drivers between 2014 and 2015?
Prepare for Any Job Assessment Test with JobTestPrep
How to Work out a Percentage Decrease or Discount
Most people are familiar with percentage decreases or discounts, as these are used in shop sales. For example, if you want to buy a new sofa and you see that the shop is offering a 40% discount, then you know that you can achieve a substantial saving over the full price of £850.
There are two ways of calculating a percentage discount. Firstly, you can calculate the discount and then subtract this from the starting price. To do this you would use the following steps:

An alternative methodology allows you to directly calculate what the new price would be (rather than the discount).
To do this you would need to use the following steps:

Suhana and Jack both want to buy a new pair of trainers. They negotiate hard and both manage to secure a discount. Suhana eventually manages to secure a 12% discount on her trainers, which originally cost £280, and Jack secures a 14% discount on his trainers with an original price of £300.
Who paid the least for their new trainers?
How much was the discount that Jack managed to secure?
Working Backwards From a Percentage
Sometimes, you may be presented with a figure that is greater than 100%.
For example, if Shimmy bought a house for £150,000 in 2010, its value may increase over the years and in 5 years’ time, it is worth 20% more than he paid for it.
The new value could be calculated by:
- Converting the percentage to a decimal: 120% = 1.2
- Multiplying the starting value by 1.2: £150,000 x 1.2 = £180,000
Therefore, in 2015 his house was worth £180,000.
You can also reverse this process and work out what the starting value may have been.
For example, Shimmy’s friend Elissa also bought a house in 2010. She recently had it valued and found it was now worth £230,000. This is 80% greater than what she originally paid for it.
To work out the original value of the house, you need to use the following process:

Grace has £3,940 in her savings account. This is 25% more than she initially invested.
How much was her initial investment?
Common Mistakes and Things to Look out For When Solving Percentage Questions
Be careful with each of the following:
-
Make sure that if you are converting decimals to percentages (or vice versa) that you get the decimal point in the right place. Often the multiple-choice answers to numerical reasoning tests will include incorrect answers with exactly this error, so if you have made this mistake there may well be an answer waiting to catch you out.
-
When comparing percentages make sure that you have a common baseline (otherwise the percentages will be unrelated to one another).
-
One area that often catches people out is year-on-year percentage increases. For example, Freya has £10 and each year this increases by 5%. How much will she have after 3 years? Some people can be tempted to add together the 5% for the 3 years i.e. 15% and multiply the £10 by 15% giving £11.5. This is incorrect. The correct way of approaching questions like this is to remember that EACH year the initial £10 increased by 5%. So at the end of year 1, Freya would have £10 x 1.05 = £10.5. At the end of year 2, she would have £10.5 x 1.05 = 11.025, and so on. It is important to add in each of these steps to arrive at the correct answer.
-
Another common error is around percentage increases. For example, the price of a loaf of bread increases by 10%. After the increase the price was £1.10, how much did the bread cost before the increase. A really common error is for people to try and solve this type of question by calculating: £1.10 x 0.9 = £0.99. This is incorrect. Remember, that £1.10 = 110%, therefore you must use this calculation: (£1.10/110) x 100 = £1.00
-
Avoid using the % button on your calculator unless you are really confident in what you are doing. It might seem like a sensible short cut but it can lead to you making basic errors.
If you would like to practise more percentage-based questions, we recommend the practice packages available from JobTestPrep. These tests include numerous percentage questions, with full explanations for all answers.




