How to Take the BMI IQ Test and Succeed (2024 Guide)
All products and services featured are independently selected by WikiJob. When you register or purchase through links on this page, we may earn a commission.
Intelligence quotient tests, or IQ tests, are the most commonly used tool to measure a person’s intelligence.
An IQ test measures the individual’s learning capacity and how they can solve problems and analyze information. An IQ test does not measure emotional intelligence or creativity.
There are a range of different IQ tests. This article will look at the Brain Metrics Initiative (BMI) IQ test – what it is, how to take it and how to succeed.
What Is the Brain Metrics Initiative?
BMI is a collaborative project committed to creating and improving intelligence and personality measurement tools, one of these being the IQ test.
What Is the BMI IQ Test?
The BMI test claims to be the most accurate online IQ test in the US. The test is created by experts in the field of IQ, and although it is a quick and relatively stress-free test, it is said to be highly accurate.
There are two different IQ tests available from BMI. The free demo test is available at the click of a button, and asks six questions, giving 10 minutes to answer them.
The demo only gives a predictive IQ score, as due to the limited set of questions, it can’t measure fully across all skills and areas.
To get a more accurate, in-depth IQ score, there is the 20-minute BMI-certified IQ test (costing $20) that consists of 20 questions. This test has a wide range of questions that enables an IQ assessment to be made.
At the end of the test, BMI provides the IQ score certificate and report of strengths and weaknesses.
Some online IQ tests are considered to exaggerate scores, whereas BMI-certified IQ tests are more comparable in the distribution of results.
The results from the BMI IQ test can be used by individuals, students, businesses and employers.
Individuals may take part for their own interest, students can show results to prospective educational institutions and employers can deduce if a candidate is suitable for a particular role.
The main skills tested are visual perception, abstract reasoning, pattern recognition, spatial orientation and analytical thinking. These areas are explained in more detail below.
Visual Perception
This type of reasoning refers to the way the brain receives, processes and organizes visual information. For example, if you see an image containing triangles of different sizes, your brain will process the different shapes, and also organize them into multiple sizes.
Visual perception concerns everything a person sees in their environment. It is useful to know your visual perception abilities as we use them every day, from analyzing a car parking space to working out puzzles and analyzing information and data at work.
Some work environments may require an in-depth analysis of a person’s visual perception to assess if they are right for the role. For instance, a driving instructor, photographer or graphic designer would need good visual perception.
Abstract Reasoning
To put it simply, abstract reasoning is the ability to understand something hypothetically. Even though a situation is real, there may be no concrete answer or outcome, so we use abstract reasoning to think about the different possibilities or what could happen. It is based on principles, concepts, ideals and symbolism.
Scientists or detectives often use abstract reasoning to reach a reasonable conclusion.
Pattern Recognition
The skill of pattern recognition is about analyzing data and identifying patterns and similarities in it. This could be in text, images or another form of data.
An up-to-date example of pattern recognition is looking at algorithms in social media. A digital-marketing expert would be able to identify the habits of a consumer by looking at their algorithms.
Pattern recognition is also used in finance and banking, any computer or data analysis role, and engineering. If you're considering studying these areas, or applying for jobs in these fields, you may want to check your pattern recognition skills first.
Spatial Orientation
Spatial orientation is the ability to mentally imagine changing and transforming objects to give a certain result, as well as being aware of the consequences of moving or rearranging something.
It is a good indicator of a person's cognitive skills, and useful in job roles such as an architect, landscaper or astronomer.
If a person is skilled at doing puzzles, drawing or building, they are likely to have good spatial awareness.
Analytical Thinking
The process of analytical thinking consists of extracting key information from data then using it to identify a solution. The data can come in the form of text, images, graphs, conversations and more.
A doctor would need to be a top analytical thinker. They identify key information from the patient and medical tests to analyze the problem, give a correct diagnosis and provide a solution.
Other roles that use analytical thinking include a mechanic, accountant and software engineer.

BMI IQ Test - Example Questions (2024)
Here are some example questions that may be asked in the BMI IQ test.
1. Look at the following sequence of numbers: 2, 3, 5, 7, 11, 13, 17, 19
Which of the numbers below would come next in the sequence?
a) 23
b) 21
c) 32
d) 45
e) 22
The correct answer is: a) 23. They are the list of prime numbers starting from 0.
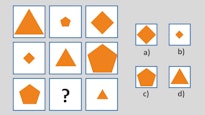
2. Please choose the box that fits the pattern
The correct answer is: a). Each row and column has a small, medium and large shape. Each also has one triangle, one diamond and one hexagon. The correct shape that fits in the gap is a large diamond.
3. What comes next in the following sequence of numbers?
1, 3, 7, 13, 21, 31, 43, 57, ?
a) 69
b) 73
c) 75
d) 62
e) 65
The correct answer is: b) 73. Each time add two more onto the difference between consecutive numbers.
How to Succeed in the BMI IQ Test in 2024
The BMI IQ test is highly thought of. However, it does differ from other IQ tests in that it doesn’t measure many linguistic or comprehension skills.
Its tests are all very similar as they look at shapes, formations and patterns. However, this can work in your favor when it comes to looking at how to succeed in this test:
Step 1. Revise What You Need to Know
As it doesn’t test much linguistics, you can focus on revising and practicing the types of questions it does ask. It’s recommended to do the free demo test and also look at example questions online.
Step 2. Identify Strengths and Weaknesses
Look carefully at questions you constantly struggle with, then read and revise these areas more than the sections where you are excelling. This will help you to give more correct answers across the whole test.
Step 3. Practice in Everyday Life
You don't need to only prepare during dedicated revision time. Do puzzles for fun, notice patterns when you are out and about, and consider spatial awareness when driving. This will all help.
Step 4. Exercise
We have all heard the phrase ‘healthy body equals healthy mind’. It really is true. Exercising regularly will also help with motivation and to alleviate stress and tiredness.
Step 5. Sleep Well
Ensure you get as much sleep as possible. This will keep your brain functioning properly and your mind focused. You will need to concentrate on the test, which will prove hard if you are tired.
Step 6. Do What Works for You
Practicing questions will indicate the best way for you to find the answer and it is important to execute this in the test. If you need to work things out on paper, or eliminate wrong answers one by one, then do so.
How Does a BMI Test Compare?
Some people express concerns over whether the BMI IQ test is legitimate since it is not established like the Stanford-Binet IQ test.
Also, as it is significantly shorter than most IQ tests, people worry that it will not give an accurate result.
There are limited questions in the BMI IQ test, which means there are some questions and areas that are not used that could further assess an individual’s IQ. However, the results it gives tally with the most established and more common IQ tests.
The fact that the questions are created by experts in the industry also adds to its good reputation.
The BMI IQ test still has the limitations of other IQ tests, and perhaps even more so as there are fewer questions.
As mentioned previously, an IQ test can only measure certain areas of intelligence. It does not assess other areas such as emotional intelligence and creativity.
Final Thoughts
The BMI IQ test is gaining in its positive reputation and has good feedback in general.
It seems to be a notable competitor in the marketplace so it is useful to prepare and be aware of it, in case it is used by an employer or other establishment.
It is affordable at $20, so it may be a good way for someone to test their IQ quickly and easily, knowing that the results are comparable to more established tests.









